今回はAI創薬の第3弾ということで、化合物の符号化(グラフ化)をやっていこうと思います!
vol.1を見ていない方は、下のリンクから見れますので是非ご覧ください。
ちなみに、統計検定の記事なども書いてますので、興味のある方は是非そちらも見てもらえたらうれしいです!
前々回の記事では、AI創薬がどのようなタスクかというところから、DeepPurposeというライブラリを使ってDavisやKIBAといったデータセットの中身を見てみました。
前回の記事では、化合物をフィンガープリントという表現で符号化しました。
今回は、化合物をグラフ表現に符号化していきたいと思います。
グラフとは
グラフ化することによって化合物を符号化するといっても、まずグラフとは何かを理解する必要があります。
離散数学における、グラフとは、頂点(ノード)と、頂点同士の関係を表したデータ構造になります。
グラフは頂点と辺という二つの構造からから構成されています。G={V,E}などと表現されます。
●頂点(ノード): V
●辺(エッジ/リンク): E(⊂V×V)
エッジが向きの情報(方向性)を持っていれば、「有向グラフ」と呼び、向きを持たなければ「無向グラフ」と呼びます。
例えば、下の図は、頂点の集合が V={1,2,3,4,5} 、辺の集合が E={(1,2),(1,3),(1,4),(3,4),(4,5)} となるグラフとなります。
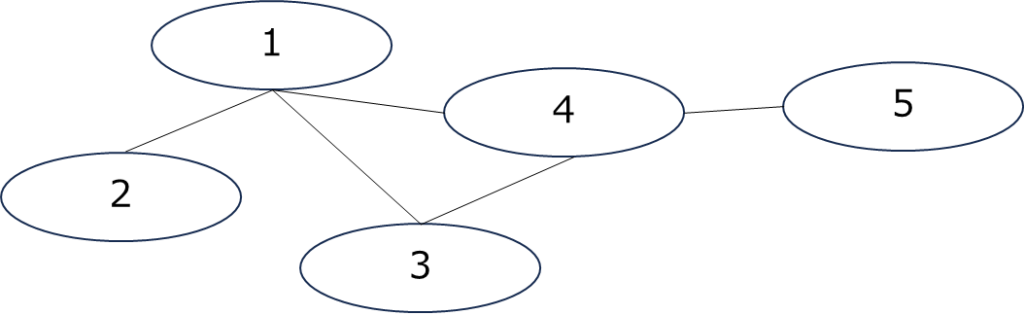
ノードを化合物、エッジを結合とみれば、化合物に見えてくると思います。化合物はその特性上、グラフ表現と相性が良いと言えます。
そして、グラフとして表現することで、グラフニューラルネットワークを利用したモデルなどを活用することができ、アフィニティの予測や化合物の特性予測でより優れた手法が続々と開発されています。
データの読み込み
前回の復習として、ライブラリのインストールと、データセットの中身を見るところまでやっていきましょう。今回はKIBAのみでやっていきます。詳しい説明は前前回の記事をご覧ください。
!pip install git+https://github.com/bp-kelley/descriptastorus
!pip install DeepPurposeimport DeepPurpose as DP
from DeepPurpose import dataset
from DeepPurpose import utils
import pandas as pd
X_drugs_K, X_targets_K, y_K = dataset.load_process_KIBA('./data/', binary = False, threshold = 9)df_KIBA = pd.DataFrame({'drugs': X_drugs_K, 'targets': X_targets_K, 'y': y_K})
df_KIBA.head()これらを実行すると、下のような出力となります。
| drugs | targets | y | |
|---|---|---|---|
| 0 | COC1=C(C=C2C(=C1)CCN=C2C3=CC(=C(C=C3)Cl)Cl)Cl | MTVKTEAAKGTLTYSRMRGMVAILIAFMKQRRMGLNDFIQKIANNS… | 11.1 |
| 1 | COC1=C(C=C2C(=C1)CCN=C2C3=CC(=C(C=C3)Cl)Cl)Cl | MSWSPSLTTQTCGAWEMKERLGTGGFGNVIRWHNQETGEQIAIKQC… | 11.1 |
| 2 | COC1=C(C=C2C(=C1)CCN=C2C3=CC(=C(C=C3)Cl)Cl)Cl | MERPPGLRPGAGGPWEMRERLGTGGFGNVCLYQHRELDLKIAIKSC… | 11.1 |
| 3 | COC1=C(C=C2C(=C1)CCN=C2C3=CC(=C(C=C3)Cl)Cl)Cl | MRPSGTAGAALLALLAALCPASRALEEKKVCQGTSNKLTQLGTFED… | 11.1 |
| 4 | COC1=C(C=C2C(=C1)CCN=C2C3=CC(=C(C=C3)Cl)Cl)Cl | MELAALCRWGLLLALLPPGAASTQVCTGTDMKLRLPASPETHLDML… | 11.1 |
前回のフィンガープリントの時と同様、化合物とタンパク質の文字列をコンピュータが処理できる形、つまり何らかの数値ベクトルに変換する必要があります。
そこで、今回はグラフによる数値化を行っていきたいと思います。
化合物をグラフに変換してみよう
RDKitというライブラリを使っていきます。RDKitはケモインフォマティクスのためのオープンソースのツールキットであり、化合物をコンピュータ上で扱うためには欠かせないライブラリとなっています。
まずはインストールしていきましょう。
!pip install rdkit次に、必要なライブラリ等をインポートしていきます。
from rdkit import Chem
from rdkit import DataStructs
from rdkit.Chem.Fingerprints import FingerprintMols
from rdkit import rdBase
from rdkit.Chem import AllChem, Draw
import numpy as npRDKitでは、化合物をMolオブジェクトとして扱われます。なので、KIBAデータセットの化合物をまとめてMolオブジェクトに変換しておきます。そして、最初の化合物を、それぞれmol1としておきます。
X_drugs_K_mol = [Chem.MolFromSmiles(X_drugs_K[i]) for i in range(len(X_drugs_K))]
mol1 = X_drugs_K_mol[0]まず、Molオブジェクトを可視化してみます。
Draw.MolsToGridImage([mol1])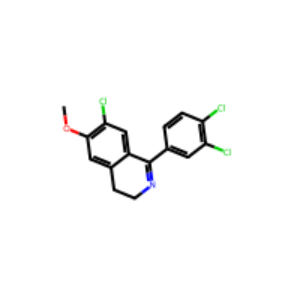
この化合物をグラフで表現してみます。
化合物をグラフで表現する上で、ここでは、二つの数値化を実践してみようと思います。
隣接行列
1つは「隣接行列」(adjacency matrix)です。
二つの原子の間に結合がある場合を1、ない場合を0とすることで、原子間の結合を対称行列で表すことができます。
たとえば、先ほどのグラフの例では、下のような隣接行列になります。

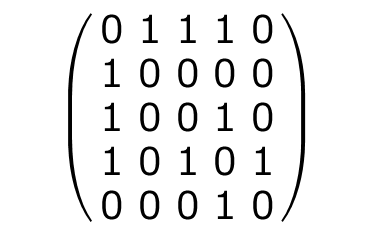
ここでは、KIBAデータの最初の化合物の隣接行列を作成してみます。
mol0 = X_drugs_K_mol[0]
# 隣接行列
admx = Chem.GetAdjacencyMatrix(mol0)
print(admx)出力は下のようになります。

無事、対象行列が生成されています。
距離行列
もう一つは「距離行列」(distance matrix)です。距離行列では、二つの原子の間の最短距離を表しています。距離行列も隣接行列同様、対象行列となります。
たとえば、先ほどのグラフの例では、下のような距離行列になります。


ここでは、KIBAデータの最初化合物の距離行列を作成してみます。
mol0 = X_drugs_K_mol[0]
# 距離行列
dimx = Chem.GetDistanceMatrix(mol0)
print(dimx)出力は下のようになります。行数が多いため途中までしかここでは載せませんが、無事、対称行列が作成されています。

グラフ構造を可視化してみよう
行列に変換することはできましたが、もう少しイメージしやすいように可視化してみようと思います。
詳しい説明は省きますが、以下のように、rdkitのDrawモジュールを使うことで、先ほどの化合物のどの原子がどのインデックスに割り当てられているかが分かります。
インデックスは0スタートで割り当てられています。
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw
from rdkit.Chem.Draw import IPythonConsole, rdMolDraw2D
from IPython.display import SVG
view = rdMolDraw2D.MolDraw2DSVG(300, 300)
option = view.drawOptions()
option.addAtomIndices=True
view.DrawMolecule(mol0)
view.FinishDrawing()
svg = view.GetDrawingText()
SVG(svg)出力は以下のようになります。右に先ほど出力した隣接行列も載せているので、見比べれば、きちんとインデックス通りになっていることが分かると思います。
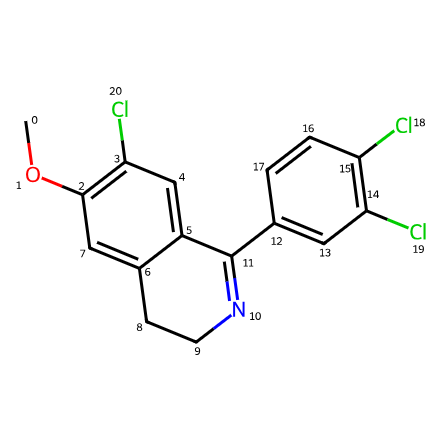

さいごに
今回は、化合物をグラフとして扱うために、隣接行列と距離行列を作成してみました。実際に機械学習モデルに入力する際には、原子の持つ情報をそれぞれのノードに持たせたり、結合の情報をエッジに持たせたりすることもあります。
ここでは、初歩的な表現として、二つの行列を作成しましたが、今度はそれぞれのノードやエッジにどのような情報を持たせるかなど解説していきたいと思います。
そうすることで、グラフ畳み込みニューラルネットなどでより効果的に学習することができます。


コメント